混合建模是一种半参数方法,它结合了知识驱动方法(参数组件)和数据驱动方法(非参数组件)的优点。这种方法可以克服纯参数方法的一些局限性。一个例子是 Monod 型方程的应用,它广泛用于开发描述生物系统的动力学模型。尽管此类模型在特定条件下获得了良好的预测,但这些模型在其它不同条件下的预测能力有限,因为它们没有考虑与细胞代谢相关的潜在机制复杂性。因此,必须开发考虑细胞代谢途径的高级动力学模型,以预测各种条件下的状态变量。然而,这些模型的构建需要对相关细胞代谢网络有详细的了解。此外,这些模型在本质上是高度参数化和非线性的,需要对细胞内和细胞外代谢物进行大量测量才能估计许多未知参数。细胞内代谢物的详细机制描述也很难构建,因为溶质转运速率受细胞膜转运蛋白的控制,并且需要考虑细胞间分布和相关的分子转运。
混合建模的一个关键优势是消除了对细胞生长、底物摄取和产物形成的显式特定速率方程的需求,因为这些参数可以通过模型的数据驱动部分进行估计。与数据驱动方法相比,这种混合方法也有好处,数据驱动方法缺乏细胞培养性能的明确物理知识,这导致在训练数据集域之外的看不见的数据预测方面表现不佳。由于来自模型参数组件的守恒方程引入的约束,混合模型还具有作为预测工具更稳健的优势。
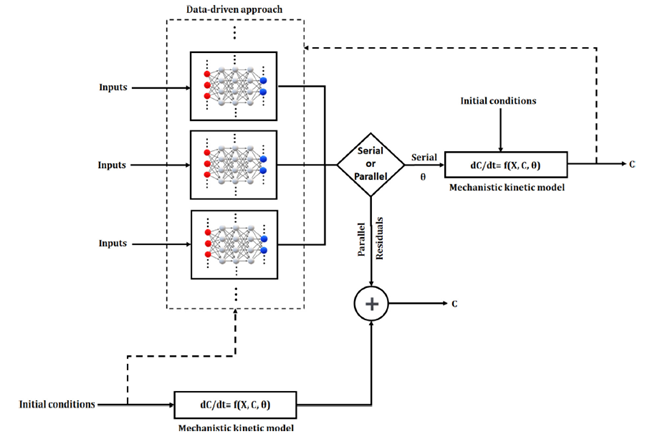
图6. 混合建模的串行和并行方法的示意图。
混合模型的配置和数学框架已在多个文献来源中进行了全面讨论。图 6 显示了可以为生化系统开发的串行和并行混合模型的典型图。混合模型的输出(例如,目标物质或代谢物浓度的向量)在此图中用 C 表示。该模型还包括数据驱动和机械组件(已指示),以及各种输入。这些可以在各种配置(串行或并行)中考虑,具体取决于数据驱动和机械组件放在一起的方式。在串行混合方法中,数据驱动模型通常用于确定完成机械动力学模型(称为部分第一原理模型)所需的未知参数(例如,图 6 中菱形右侧的矢量𝜃)。相反,当机械动力学模型不准确时,通常应用并行混合方法。因此,一个数据驱动的框架被训练来预测实验数据和机械动力学模型估计的相应值之间的残差(见图 6 中的平行残差)。因此,惩罚项适用并抵消任何不准确的估计。由于从生物反应器获得的数据通常包括细胞和代谢物浓度的时程变化,因此初始条件被用作机械模型的输入来求解时间相关的动力学方程(见图 6)。
动物和微生物细胞培养混合建模的一种常用方法是将源自守恒方程和动力学表达式的第一原理模型与人工神经网络相结合,以串行配置的方式对特定速率进行数据驱动预测。通常,该模型的数据驱动组件缺乏特定速率的直接测量,即训练和获取网络可训练变量所需的数据,即权重和偏差。为了解决这个问题,提出了两种策略
生物反应速率的近似值,其中使用实验浓度与时间的关系曲线,然后最小化预测的特定速率和近似值之间的误差;以及
一种灵敏度方法,其中预测浓度和真实浓度之间的误差被最小化。由于数据驱动组件的输出是特定速率(而不是浓度),因此网络可训练变量与浓度之间的明确关系是未知的。因此,浓度相对于特定速率的梯度用于搜索可最小化预测浓度和真实浓度之间的误差的网络可训练变量。
文献中使用了不同的近似方法来估计基于实验数据的生物反应速率值。参数估计技术、多项式回归模型、三次样条函数和 Tikhonov 正则化是此类方法的示例。然而,数据中的噪声可能导致不准确的速率估计,因此需要进行平滑处理。灵敏度方法更能抑制噪声;尽管如此,由于大量的计算成本,将这种方法用于需要大量超参数优化的大型训练数据集和训练算法可能具有挑战性。
许多研究人员研究了具有不同微生物培养物的生物反应器的混合建模,例如大肠杆菌的蛋白质生产、聚羟基脂肪酸酯(恶臭假单胞菌Pseudomonas putida生产 PHA,肠杆菌 A47 生产胞外多糖 (EPS),黑曲霉Aspergillus niger发酵葡萄糖酸钠以及Kluyveromyces marxianus酵母生产菊糖酶等),表明了混合建模方法的广泛潜力。
此外,混合模型中可以包含多个神经网络,每个神经网络都特定于特定的反应速率。多个神经网络的使用在设计网络架构和超参数优化方面提供了增强的灵活性,以及更适当地选择对特定速率有显著影响的重要输入。
作为一个典型的例子,Laursen 等人(2007)基于工业数据成功开发了一种混合模型,用于使用大肠杆菌细胞在补料分批发酵中生产外来蛋白质。作者使用不同的神经网络来估计特定速率,包括生长速率、葡萄糖和氧气消耗速率,以及乙酸盐和蛋白质生成速率。测量值(例如生物量浓度)用于生成神经网络的训练数据。此外,网络预测的性能使用不同的输入进行了测试,例如葡萄糖浓度、生物量浓度、氧饱和度百分比和蛋白质浓度。该研究表明,与将葡萄糖浓度用作唯一输入的网络相比,当细胞、葡萄糖和蛋白质的浓度包含在输入层中时,可以更准确地预测特异性生长速率。该结果还表明,人工神经网络可用于更准确地捕获特定速率的准确函数,与仅描述细胞生长对底物浓度的依赖性的简单经典 Monod 方程相比,这是一个明显的优势。
此外,还开发了各种混合模型来监测、控制、预测和优化哺乳动物细胞培养。在 Dors 等人(1996)开发的混合模型中,将哺乳动物细胞培养的改良 Monod 型相关性与神经网络方法相结合,其中包括基于模糊变量的加权方法来估计每种方法的相对重要性。这允许分配给经典 Monod 方法的权重发生变化,因为神经网络的可预测性受到训练数据的限制,允许在一些测量数据可用时增加权重。在另一项研究中,新陈代谢、运输现象和经验过程数据的先验知识被整合到一个混合模型中,用于哺乳动物细胞生物反应器的在线优化和控制。描述细胞外成分的宏观反应是使用由机械和经验函数定义的基本通量分析得出的。具有单个隐藏层的反向传播神经网络用于估计未知反应速率的向量。然后成功地使用混合模型来优化抗体生产。
混合方法优势的另一个例子是,人工神经网络可用于确定特定速率对不同生物反应器过程变量的复杂依赖性,对其而言,很难得出直接的动力学相关性。例如,Narayanan 等人 (2019) 在细胞培养的不同成分上使用简单的质量平衡来预测单克隆抗体滴度的时程变化。在这项研究中,建立了一个神经网络来估计特定速率作为实验数据的函数。它还包括设计条件,如溶氧设定点、动态变化、非受控过程变量,如活细胞密度和受控过程变量,如 pH 值。作者表明,与统计预测模型相比,这种混合模型可以更稳健地预测滴度。
原文:M. K. Alavijeh, I. Baker, Y. Y. Lee, et al., Digitally enabled approaches for the scale up of mammalian cell bioreactors, Digital Chemical Engineering 4 (2022) 100040






